In this experiment, we performed Discrete Fourier Transform of 4-point sequence, zero padded signal, and Expanded signal. Magnitude spectrum of each case was drawn and observed that DFT coefficients are defined for w=2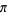
k/n. Also the spectrum is discrete in the range 0 to 2.From the three cases when the signal was zero padded the length of the signal increased due to which frequency spacing got decreased which increases the Resolution the spectrum.Also, expansion of signal in time domain gives compressed spectra in Frequency domain.We also observed that DFT produces periodic Results.Computations in DFT which included real Multiplication and Additions was also Calculated and we found that Discrete Fourier Transform is slow.
k/n. Also the spectrum is discrete in the range 0 to 2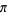.From the three cases when the signal was zero padded the length of the signal increased due to which frequency spacing got decreased which increases the Resolution the spectrum.Also, expansion of signal in time domain gives compressed spectra in Frequency domain.We also observed that DFT produces periodic Results.Computations in DFT which included real Multiplication and Additions was also Calculated and we found that Discrete Fourier Transform is slow. 
DFT can be used efficiently to perform convolution and correlation
ReplyDeleteThe Discrete Fourier transform (DFT) converts a finite sequence of equally spaced samples of a function into the list of coefficients of a finite combination of complex sinusoids, ordered by their frequencies, that has similar sample values.
ReplyDeleteDFT though a simpler method, FFT has less number of complex and real multiplications and additions so it is preferred
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteThe magnitude spectrum is periodic due to the characteristic of twiddle factor
ReplyDeleteDFT is nothing but sampling DTFT in frequency domain.and spectrum of DFT is discrete since input is periodic.
ReplyDeleteIt can also provide uniformly spaced samples of the continuous DTFT of a finite length sequence.
ReplyDeleteDigital domain requires samples of the signal in frequency domain. We use DTFT to convert the analog signal to digital signal and use DFT to get samples of it.
ReplyDeleteThe twiddle factors all lie on a unit circle; so the more the samples, the more that circle becomes complete, and hence the resolution gets better.
ReplyDelete